Introdução

Sou estudante do curso Bacharelado Interdisciplinar em Ciência e Tecnologia, da Universidade Federal do Maranhão. Para meu trabalho de conclusão de curso decidi realizar um levantamento sobre os mecanismos que permitem um computador jogar xadrez. O contexto desse trabalho é, portanto, o campo da inteligência artificial.

E, para o xadrez, o estado da arte é uso de redes neurais. A cena do xadrez foi abalada por volta de 2017 quando o Google divulgou um mecanismo chamado Alphazero, uma rede neural artificial que aprendeu a jogar xadrez sozinha jogando contra si própria e, em algumas horas, foi capaz de adquirir um nível de jogo para bater o melhor software de xadrez daquela época, o Sotckfish, que usava outras técnicas para jogar.

Nesse post eu descrevo de maneira muito objetiva como um computador consegue jogar xadrez sem entrar em detalhes de implementação. Existe um universo de técnicas e métodos que podem ser usados. Vou focar em mostrar que a ideia básica para o computador decidir qual movimento realizar não é complicada de entender e pode ser utilizada para qualquer jogo minimamente parecido com o xadrez.

Eu considero que o leitor já possui alguma familiaridade com o jogo, conhecendo o movimento das peças, as regras básicas, movimentos especiais como roque e en passant, etc., de modo que não vou adentrar nesses detalhes. No entanto, vou destacar as regras que determinam o final do jogo, seja com vitória, ou com empate. Entender bem essas situações será importante mais à frente.

Vencendo a partida

Para vencer uma partida é necessário aplicar xeque-mate no rei adversário. O xeque-mate é uma condição em que o rei está sob ataque direto e não há nenhum movimento que o jogador possa realizar para tirar seu rei do ataque.

Também é possível vencer quando o tempo do oponente acaba. Isso acontece com frequência em partidas online e em partidas de torneios com controle de tempo, bem como qualquer partida jogada entre duas pessoas, por exemplo, onde elas usam relógio. Os jogadores se alternam para movimentar as peças e aquele que está na vez tem um relógio atribuído a si com uma quantidade de tempo pré-estabelecido que vai diminuindo até que o lance seja realizado. Uma vez que o lance é feito, o relógio de um jogador trava e começa a contar o relógio do outro jogador. Se o tempo de um jogador acabar, ele perde a partida.

Empatando a partida

No xadrez, a partida também pode terminar em empate. O jogo pode empatar quando um jogador não tem movimentos válidos, mas o seu rei não está atacado. Nessas situações, diz-se o rei ficou afogado. Se não tem xeque-mate, então não há vitória.

Na partida abaixo, jogada entre Lukany e Smulyan em 1938, é a vez das peças pretas realizarem o movimento e elas estão em severa desvantagem material. Basicamente, as peças brancas conseguiriam promover um dos peões e aplicar xeque-mate em mais alguns lances. No entanto, o jogador de pretas movimenta o peão da casa a6 para b5 e empata a partida. Não há o que o jogador das peças brancas possa fazer, pois com qualquer movimento, na próxima jogada, as peças pretas estariam sem movimentos disponíveis e o rei não estaria atacado de forma direta, configurando empate por afogamento.

Outra situação para o empate, conforme estabelecido pela Federação Internacional de Xadrez – FIDE, é a repetição movimentos. Aqui, um jogador pode reivindicar o empate quando uma mesma posição, isto é, a disposição das peças no tabuleiro, se repetir por três vezes, podendo essas posições terem acontecido em qualquer momento da partida.

Além disso, a partida de xadrez não pode se prolongar indefinidamente, seja porque há uma quantidade de tempo limitada, mas também uma quantidade limitada de movimentos que um jogador pode realizar. A FIDE estabelece que o xeque-mate deve acontecer em até 50 lances, desde que nenhum peão seja movimentado, ou uma captura de peça seja realizada, pois esses movimentos fazem com que a contagem dos 50 lances volte ao início. Isso força o jogo a terminar em algum momento. Se a contagem chegar nos 50 lances, um jogador pode reivindicar o empate.

Essas situações são, por vezes, utilizadas quando um jogador está em desvantagem material, mas percebe uma maneira de forçar as repetições de uma posição, ou escapar do xeque-mate durante 50 lances.

Existem outras situações teóricas onde não é possível aplicar xeque-mate. A mais trivial é quando restam apenas os dois reis no tabuleiro, ou quando, mesmo com algumas peças, não é possível forçar a vitória. É o caso de um rei e dois cavalos contra um rei, onde os cavalos não conseguem vencer a partida de maneira forçada (o xeque-mate é possível, mas o rei em desvantagem teria que realizar movimentos que permitisse a derrota).

Resolvendo o Xadrez Matematicamente

A teoria matemática dos jogos é um ramo da economia, onde um ambiente com múltiplos agentes realizam ações que afetam seus participantes, não importante se estes agentes são cooperativos ou competitivos. Para esse contexto, dá-se o nome de jogo. Em ambientes com muito, muitos agentes, é mais comum chamar de “economia”.

E o xadrez é isso: um jogo onde dois agentes, comumente chamados de jogadores, realizam ações de maneira alternada com objetivo de ganhar a partida prendendo o rei adversário. Jogos desse tipo tem algumas características. Para o xadrez, uma delas é que ele é um jogo de informação completa, pois cada jogador tem toda informação necessária e ela está disponível no tabuleiro. Outra característica é que o xadrez é um jogo de soma zero, pois o ganho de um jogador representa uma perda de tamanho equivalente para o outro jogador, isto é, quando um jogador ganha, o outro necessariamente perde, ou quando um jogador empata, o outro também empata, ou, ainda, se um jogador está um pouco melhor, o outro está pouco pior, sempre em níveis iguais, mas opostos.

Mais acima foi citado que entender como um computador pode jogar xadrez não é uma tarefa complicada. Vamos compreender, então, quais mecanismos mais básicos para alcançar esse objetivo.

Primeiramente, precisamos definir o conceito de “movimento ótimo” e criar um mecanismo para encontrá-lo. Essa parte, pelo menos na teoria, é muito fácil de entender. Vamos ver o porquê.

Um movimento ótimo é aquele que vai levar à vitória, ou então, ao melhor resultado possível, por exemplo, o empate quando a vitória não é factível. Determinar esses resultados é bastante simples porque as posições de xeque-mate e empate são possíveis de verificar diretamente no tabuleiro. Assim, em uma disposição qualquer de peças, um bom algoritmo (teoricamente) deve ser capaz de testar todas as possibilidades de movimentos que levam ao xeque-mate no rei adversário, ou pelo menos ao empate.

A imagem a seguir ilustra como esse pensamento de busca pelo movimento ótimo é implementado. Nela, uma posição é apresentada e é a vez das peças pretas jogarem. Mas qual é o melhor lance? O melhor lance pode ser encontrado depois que uma busca é realizada em todos os movimentos possíveis a partir da posição inicial e, para cada uma dessas possibilidades, novos movimentos são testados, assim em diante, até que se chegue em uma posição de vitória. O dispositivo computacional testa todos os arranjos de peças fazendo simulações de movimentos e uma representação natural para essa busca é uma árvore. Nessa árvore, cada nó é um possível arranjo de peças gerado com um movimento de peça a partir de uma posição anterior. Os nós terminais, ou folhas, dessa árvore são as posições de xeque-mate ou de empate. Lembrando que pela regra das três repetições, ou pela regra dos 50 lances, essa árvore não cresce indefinidamente. Assim, qualquer caminho em profundidade dentro dessa árvore que leva a um nó de xeque-mate representa uma sequência de movimentos ótimos e, havendo múltiplos caminhos que levam à vitória, podemos ainda escolher aquele que faz o menor número de movimentos. A imagem abaixo mostra duas posições de xeque-mate com os tabuleiros contornados em vermelho. Com isso, basta o computador realizar os movimentos que levam aos nós que indicam xeque-mate. No caso de o xeque-mate não ser possível, uma alternativa é encontrar o caminho que vai mais profundamente na árvore, pois isso aumenta o tempo de sobrevivência.

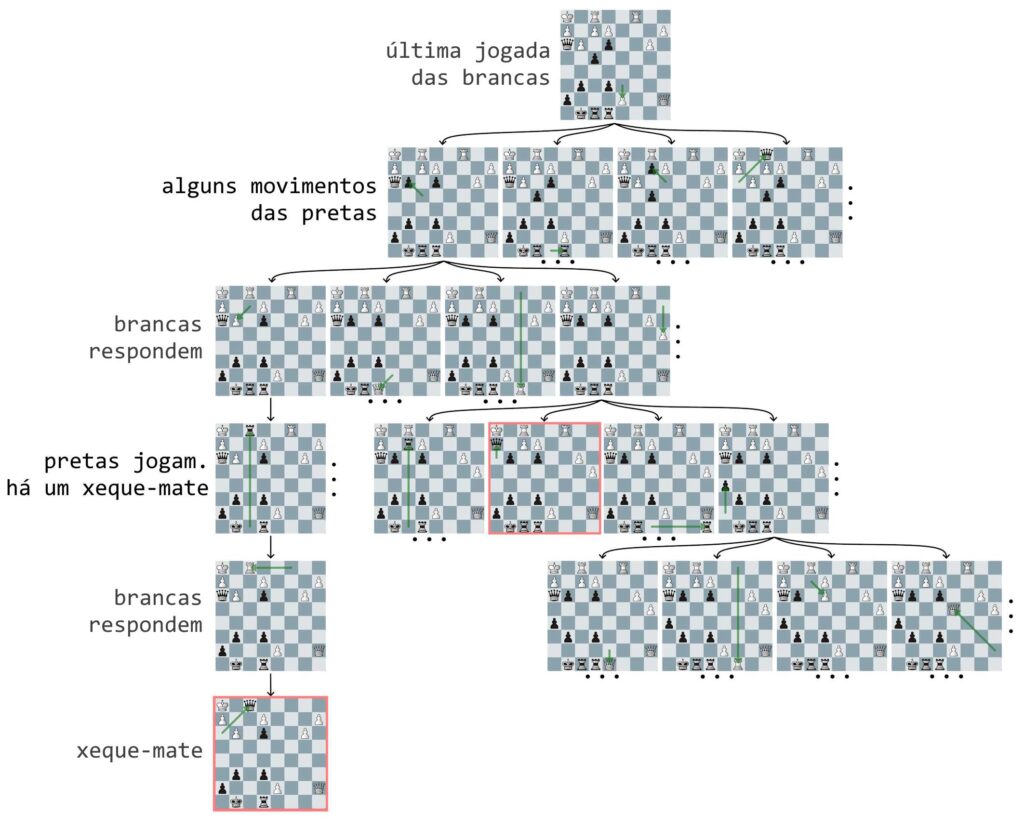
E é simples assim que, matematicamente, um computador pode jogar xadrez: montar a árvore de movimentos e realizar a sequência de movimentos que levam aos nós de xeque-mate.

No entanto, aparentemente é IMPOSSÍVEL implementar essa solução computacionalmente. No xadrez, a média de ramificações gira em torno de 35, isso quer dizer que, para uma dada disposição de peças, existem 35 movimentos possíveis. Uma partida típica de xadrez vai até o lance 50. Então imagine, para cada movimento realizado, outros 35 são possíveis, gerando novas posições totalmente diferente das anteriores. Só até o lance 15, são 2015099950053364471960 de posições diferentes. No final, a estimativa é que existem 10154 posições na árvore de movimentos para o xadrez. Para ter uma ideia do quão absurdamente grande é esse número, outra estimativa interessante é que existem apenas algo entre 1078 e 1082 átomos em todo universo observável.

Função de Avaliação

Para contornar o problema sobre a quantidade de posições do xadrez, continuamos com a ideia inicial de montar uma árvore com os movimentos, mas agora não vamos até o final dela. Essa solução, no entanto, gera outro problema.

Antes, na teoria, bastava percorrer a árvore até encontrar os nós com posições de xeque-mate. Mas não sendo possível percorrer a árvore inteira, devemos usar outra estratégia para avaliar um nó dessa árvore. Assim, a busca pela melhor posição vai somente até uma determinada profundidade, até onde é computacionalmente viável, ou até onde for possível usando qualquer métrica limitante, como o tempo em partidas com controle de tempo.

Introduz-se então o conceito de “função de avaliação”. O objetivo dessa função é avaliar uma posição específica, entregando um valor numérico sobre o quão boa é essa posição para o jogador de peças brancas ou para o jogador de peças pretas. Com esse conceito, se a função calcular, por exemplo, um valor 3 para uma posição e 5 para uma outra, significa que a sequência de movimentos que leva até a posição que vale 5 é mais propícia à vitória.

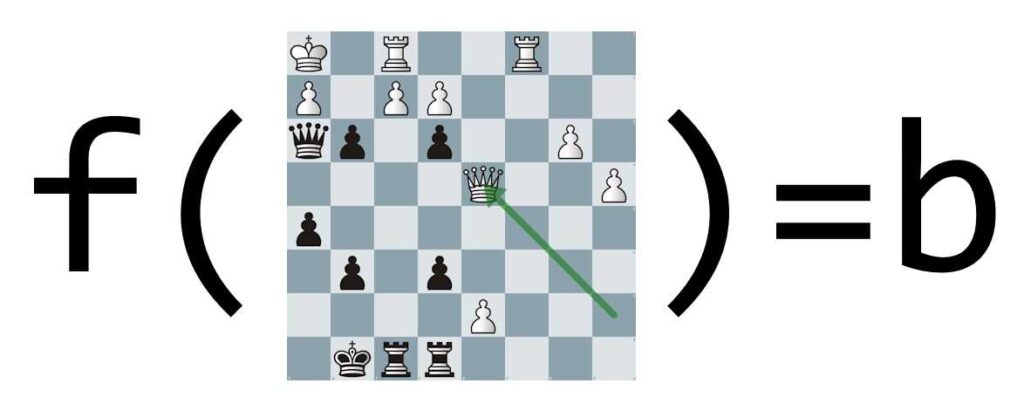
A imagem acima ilustra esse pensamento, onde uma função f recebe como argumento uma posição qualquer e tem o objetivo de determinar o valor b indicativo do quanto essa posição é boa para o jogador interessado.

No entanto, avaliar uma posição de forma numérica não é uma tarefa fácil, mas existem diversas maneiras de descrever uma posição em termos de um valor numérico. É muito comum, para quem começa a jogar xadrez, aprender sobre o valor absoluto de cada peça. É como um número que indica a força de cada uma delas. Os valores comumente utilizados são:

  • Peão – vale 1 ponto
  • Cavalo – vale 3 pontos
  • Bispo – vale 3 pontos
  • Torre – vale 5 pontos
  • Dama – vale 9 pontos
  • Rei – não possui um valor definido, pois sua captura resulta no fim do jogo

Com isso, muitas vezes, não é vantajoso capturar um bispo inimigo utilizando uma torre se essa torre for capturada em seguida pelo oponente. O peão, embora tenha pontuação absoluta de 1 ponto, cada jogador inicia o jogo com 8 deles. É importante, entretanto, sinalizar que essas pontuações são valores que sozinhos não dizem muito sobre a força de uma posição.

Em uma partida existem dezenas, até mesmo centenas de fatores que, em conjunto, determinam qual lado está em vantagem. O valor absoluto das peças é apenas um desses fatores. O bispo, por exemplo, embora tenha pontuação absoluta semelhante ao cavalo, em posições abertas, quando ele consegue mover uma grande quantidade de casas, pode ter uma força relativa maior que o cavalo. Por outro lado, em posições fechadas, com pouco espaço para movimentação, a característica do cavalo saltar sobre outras peças pode ser uma vantagem, realizando suas manobras em forma de “L”. Há também um entendimento que qum par de bispos é mais forte que um bispo e cavalo.

Outro aspecto que pode ser avaliado é a estrutura de peões. Existem muitos livros com centenas e até milhares de páginas apenas sobre o estudo da estrutura dos peões, seus posicionamentos, se estão juntos, se há dois ou três peões na mesma coluna. Outro tema é a torre na sétima horizontal, um conceito bem conhecido para quem já tem alguma prática com o jogo. A exposição do rei também é um tema que pode ser considerado. A mobilidade das peças, isto é, quantos movimentos válidos um jogador tem à sua disposição é mais um fator a ser considerado. Enfim, qualquer aspecto que um ser humano considera ao avaliar uma posição pode ser traduzido para o computador e utilizado para determinar quão boa é a posição.

A função de avaliação de uma posição, portanto, pode ser tão boa quanto forem as regras implementadas nela. Com essas regras estabelecidas, utilizamos a ideia de percorrer a árvore de movimentos até certo nível e aplicar a função de avaliação, por exemplo, em cada nó desse nível. Os nós que trouxerem a melhor pontuação serão aqueles cujo caminho será utilizado para aprofundar ainda mais a busca. Com isso, a ideia de movimento ótimo para a vitória passa a ser a busca por um movimento capaz de maximizar o ganho baseado em diversas heurísticas.

A imagem abaixo ilustra essa estratégia. As peças brancas precisam determinar a melhor jogada. A árvore de movimentos é montada até certo nível, onde a função de avaliação é aplicada, encontrando alguns nós promissores (marcados em verde). A partir desses nós, a busca continua ainda mais profundamente, até que se chegue em determinado nível. Mais uma vez, os nós mais promissores estão marcados em verde, com pontuação 7 e 8 no exemplo. O dispositivo computacional pode, então, realizar o movimento cujo caminho na árvore leva até esses nós.

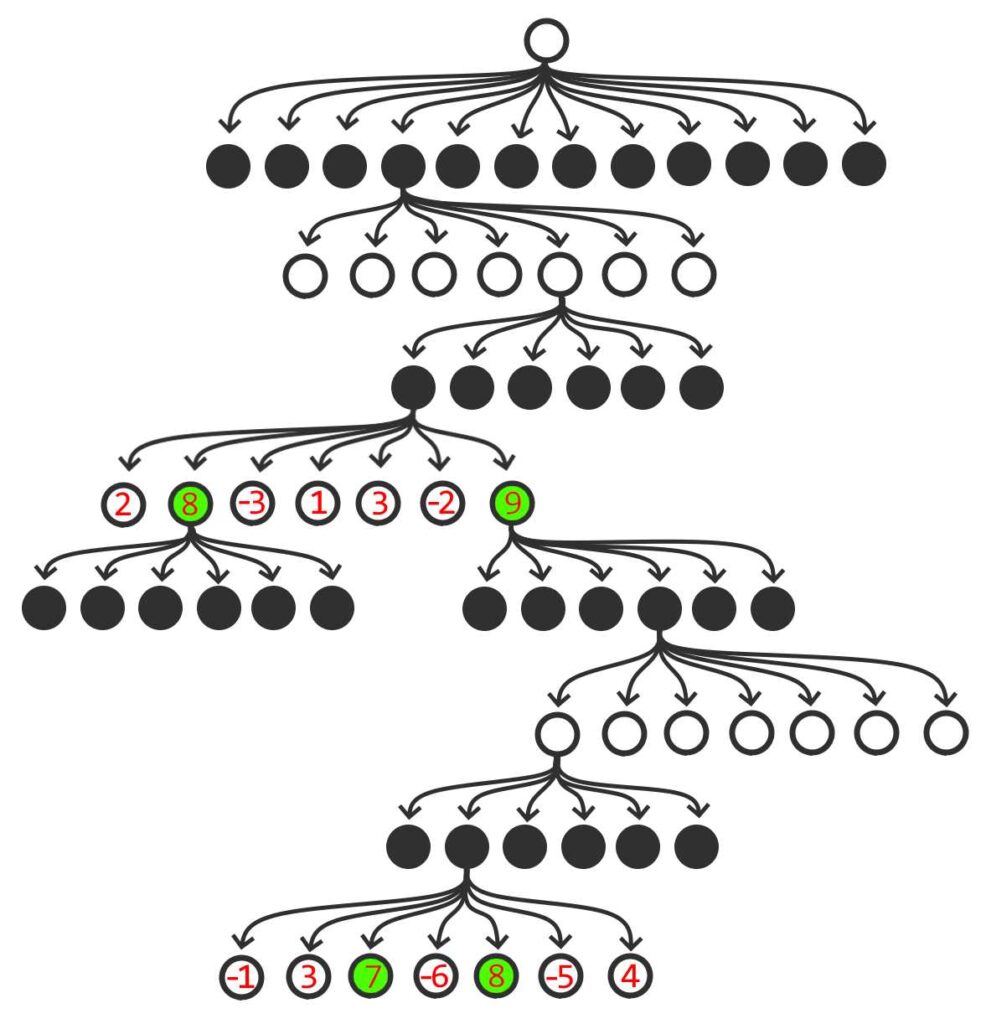
Essas pontuações são baseadas em heurísticas. Por exemplo, sabe-se que colocar uma torre em uma coluna aberta, isto é, uma coluna sem peões, é um movimento muitas vezes bastante adequado para se adquirir poder posicional. Para traduzir esse comportamento para um modele computacional, devemos atribuir uma pontuação para a torre posicionada na coluna aberta. Mas qual pontuação? Uma pontuação muito alta pode forçar o computador a sempre fazer esse movimento de torre em detrimento de outros movimentos melhores. Por outro lado, uma pontuação baixa demais pode fazer com que o computador ignore essa possibilidade que é sabidamente boa em diversas situações. Uma forma de encontrar a pontuação mais adequada é realizar diversos testes. Por exemplo, em uma versão do algoritmo, atribui-se uma pontuação, digamos, de 6 pontos para uma torre posicionada em coluna aberta e, em outra versão, atribui-se uma pontuação, digamos, de 3 pontos. Ambas as versões jogam entre si e aquela que ganhar mais partidas indica qual a pontuação é mais adequada. Essa estratégia pode ser utilizada para todos os aspectos utilizados na função de avaliação que determina o quão boa é uma posição no xadrez.

O que foi apresentado até aqui, de maneira geral, permite o computador jogar xadrez. No entanto, o estabelecimento das heurísticas que determinam o quão boa é uma posição dependem de conhecimento humano previamente adquirido e traduzido para um modelo computacional. Dessa forma, o computador é capaz de jogar partidas em níveis criativos até onde um humano também é capaz de instruí-lo. Mas, claro, o computador sempre tem a vantagem de ser muito mais rápido.

As ideias apresentadas até aqui são o que há de mais fundamental na programação de computadores para jogar xadrez, ou qualquer outro jogo de turno, como jogo da velha e damas e podem ser estendidas para jogos com mais jogadores. Essas técnicas também servem para jogos de cartas, como o poker, que não é um jogo de informação completa como o xadrez, pois um jogador não conhece as cartas do outro e, inclusive, possui aspectos probabilísticos.

Redes Neurais

Vimos que a definição de uma função de avaliação da posição depende muito de conhecimento prévio sobre o xadrez. Cada aspecto que define uma posição é minuciosamente programado. E durante muito tempo essa foi a técnica mais utilizada. O super computador Deep Blue, por exemplo, consistia em um poderoso conjunto de software e hardware construído especialmente para jogar xadrez. Seus processadores tinham circuitos especializados para o cálculo de posições e geração de movimentos. Foi o primeiro computador a conseguir vencer um jogador de elite em 1997, quando superou o campeão mundial de xadrez, Garry Kasparov.

Em 2016, a empresa DeepMind, uma subsidiária da Alphabet (empresa mãe do Google) concluiu o desenvolvimento de um programa de computador para jogar Go, um jogo muito popular no leste asiático. À época, o Go representava um grande desafio para o campo da inteligência artificial devido o gigantesco número de possibilidades. Enquanto que, no xadrez, o fator de ramificação é 35, no Go, estima-se um fator de 250. Utilizando técnicas comuns, não existia algoritmo capaz de vencer jogadores de elite.

O modelo construído pela DeepMind, baseado em redes neurais artificiais, ganhou destaque mundial ao conseguir vencer um dos maiores jogadores de Go do mundo. Há um documentário muito bom na NetFlix chamado ALPHAGO que acompanha a construção desse sistema e o confronto com Lee Sedol, um dos jogadores de Go mais renomados e talentosos do mundo.

Mais tarde, a DeepMind desenvolveu o AlphaZero, uma generalização do AlphaGo, mas agora capaz de jogar xadrez e shogi. O método diferenciado levou a novas percepções e abordagens estratégicas no xadrez e fez com que o AlphaZero se tornasse um dos melhores jogadores de xadrez computacionais do mundo em um curto espaço de tempo.

Em vez de ser programado com cetenas de heurísticas e com uma grande base de dados de partidas de xadrez jogadas por humanos, como era comum, o AlphaZero aprendeu a jogar xadrez sozinho, jogando milhões de partidas contra si mesmo e usando aprendizado por reforço para melhorar continuamente.

No modelo do AlphaZero, não existe mais o papel de uma complexa função de avaliação codificada manualmente, baseada na atribuição de valores a diferentes posições no tabuleiro. O AlphaZero utiliza sua rede neural para avaliar posições, o que lhe permite ter uma percepção mais completa e estratégica do jogo. A rede, treinada com milhões de partidas, consegue aprender aspectos determinantes de uma posição que nem mesmo os melhores jogadores humanos conseguiriam imaginar. A rede neural desenvolveu um estilo de jogo que muitos observadores descreveram como mais humano do que outros softwares de xadrez tradicionais. Ela frequentemente optava por movimentos e estratégias que priorizavam a atividade e a iniciativa, mesmo que isso significasse sacrificar material.

Para testar o AlphaZero, a DeepMind o colocou para jogar 100 partidas contra o melhor software da época, o Stockfish. No confronto, AlphaZero ganhou 28 partidas, e houve 72 empates (nenhuma vitória do Stockfish).

Funcionamento

O AlphaZero utiliza uma rede neural profunda para avaliar uma posição. A rede começa sem nenhum conhecimento do jogo, exceto as regras fundamentais. Como dito, o sistema joga contra si mesmo milhões de vezes, atualizando sua rede neural após cada jogo para melhorar suas políticas de movimento e avaliações. Essa técnica permite que ele aprenda as melhores estratégias apenas pela experiência.

O AlphaZero usa Monte Carlo Tree Search – MCTS – para explorar as possibilidades de movimento. A pesquisa começa a partir da posição atual do tabuleiro e simula jogos até o final, usando a rede neural para guiar as simulações e avaliar as posições. A MCTS, orientada pela rede neural, permite que o AlphaZero avalie movimentos de forma muito mais eficiente e profunda do que os motores tradicionais.

Simular partidas até o final é uma tarefa computacionalmente custosa. O AlphaZero faz uso intenso de TPUs (Tensor Processing Units) desenvolvidas pelo Google, otimizadas para operações de redes neurais. Isso lhe permite avaliar milhões de posições rapidamente. Note que, simular partidas até o final não significa completar toda a árvore de possibilidades do xadrez. Usando o MCTS, o AlphaZero simula a partida inteira até uma determinada profundidade, depois escolhe as posições mais promissoras e continua a simulação, repetindo o processo até chegar situações de fim de jogo. Todo esse processo é realizado com uma mesma rede neural. A atualização é realizada após o final da partida.

Impacto no Mundo do Xadrez

Tradicionalmente, os softwares de xadrez se baseavam em uma combinação algoritmos de busca, tabelas de finais, livros de abertura, e heurísticas cuidadosamente afinadas. O AlphaZero, em contraste, usou aprendizado por reforço e redes neurais profundas, aprendendo o jogo do zero. Esta abordagem de aprendizado de máquina era revolucionária no xadrez computacional.

O AlphaZero apresentou novas ideias em várias aberturas estabelecidas, trazendo novidades e revigorando linhas que eram consideradas menos populares ou até mesmo inferiores. A comunidade de xadrez estudou profundamente suas partidas para obter novas ideias.

O sucesso do AlphaZero estimulou interesse em técnicas de aprendizado por reforço e redes neurais no xadrez computacional. Ele mostrou que era possível obter um desempenho super-humano sem depender de décadas de conhecimento e heurísticas específicas do domínio.

A abordagem do AlphaZero inspirou o desenvolvimento e a evolução de outros motores de xadrez. Por exemplo, o projeto Stockfish, um dos principais softwares de xadrez de código aberto, incorporou técnicas de aprendizado profundo em variantes do motor, resultando em melhorias de desempenho.

A introdução do AlphaZero gerou um debate saudável sobre as vantagens e limitações das abordagens tradicionais de programação de xadrez em comparação com as técnicas de aprendizado de máquina. Isso levou a uma maior experimentação e fusão de abordagens. O confronto entre o AlphaZero e o Stockfish, e a subsequente análise e discussão, atraiu a atenção do público e popularizou ainda mais o xadrez e a pesquisa em inteligência artificial.

Base de Finais

Ainda dentro dos mecanismos computacionais para jogar xadrez, existem as bases de finais. São listagens pré processadas de movimentos que resultam em xeque-mate ou empate. Para qualquer posição com até sete peças no tabuleiro, incluindo os reis, o xadrez já foi resolvido. Assim, é possível determinar se a posição vai resultar em vitória, ou empate, e quais movimentos seguem para cada um dos resultados. A quantidade diminuída peças dar o nome dessas bases, “de finais”.

Uma dessas bases é a Syzygy, que possui absurdos 423836835667331 de posições únicas catalogadas (isso é quase nada se comparado a 10154), distribuídas em 18 TB de arquivos; é cerca de 0,35 bit por posição. Essa base é capaz de listar todos os movimentos de uma posição até chegar em qualquer resultado.

As bases de finais mostram os limites do xadrez. Por exemplo, na posição abaixo, as peças brancas conseguem aplicar xeque-mate depois de 1034 lances. A dama e o cavalo das peças brancas precisam fazer diversas manobras até conseguirem neutralizar a torre, o cavalo e bispo do oponente. Isso é muito mais que os 50 lances permitidos pela regra do empate estabelecida pela FIDE. Os mistérios do xadrez vão além de qualquer capacidade humana.

Conclusão

Exploramos neste texto os alguns dos mecanismos que permitem que um computador jogue xadrez. Desde a definição de um movimento ótimo para resolver o xadrez matematicamente, mas também o conceito de função de avaliação, uma vez que não factível cobrir todas as possibilidades do jogo. Também, com o uso de redes neurais, vimos como a inteligência artificial revolucionou o campo do xadrez computacional. O AlphaZero, em particular, trouxe uma abordagem inovadora, aprendendo a jogar xadrez de maneira autônoma, sem depender de heurísticas humanas pré-programadas. Sua capacidade de superar os melhores programas de xadrez da época e suas aberturas criativas inspiraram a comunidade de xadrez a explorar novos horizontes.

Além disso, discutimos o papel das bases de finais, que representam uma fonte valiosa de conhecimento sobre o xadrez. Essas bases pré-processadas, como a Syzygy, possibilitam a análise detalhada de posições complexas e a determinação de resultados, revelando os limites do jogo.

Em resumo, a combinação de algoritmos de busca, redes neurais, aprendizado por reforço e bases de finais está transformando a maneira como compreendemos e jogamos xadrez. A inteligência artificial, com sua capacidade de avaliação e aprendizado, está moldando o futuro do jogo e desafiando as fronteiras do conhecimento humano neste jogo milenar.

Referências

Categorized in:

Inteligência Artificial,

Last Update: 18/01/2024

Tagged in:

, , , , , ,