Introdução
A Tabela Price é um método de amortização de empréstimo que propicia pagamento de parcelas iguais. Assim, dada uma taxa de juros aplicada sobre um montante a ser financiado, o método Price permite pagamento com valor constante e o saldo devedor é zerado após o pagamento da última parcela.
Existe uma fórmula para caluclar o valor da parcela:
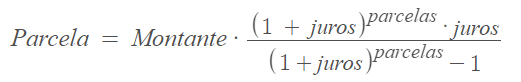
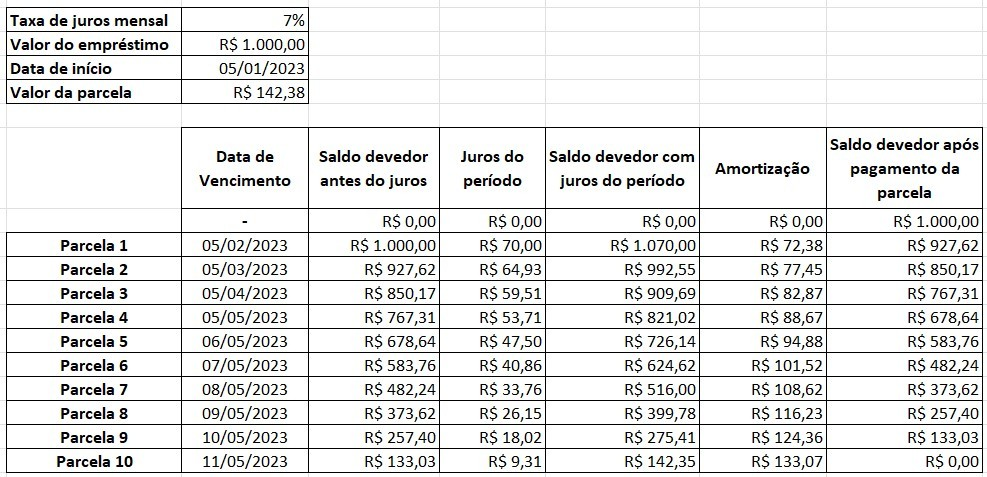
No exemplo a seguir, simplesmente aplicando aplicando a fórmula em um valor de R$ 1000,00 parcelados em 10 vezes a uma taxa de juros de 7% ao mês, chegamos em um valor de parcela de R$ 142.38. Ao final do pagamento da última parcela, o saldo devedor está zerado.
Limitações da fórmula
Na prática, a fórmula apresentada possui algumas limitaçoes, dependendo de como o juros é aplicado. A primeira delas é que o período de tempo entre o pagameto das parcelas deve ser igual. Note que, quando falamos que um empréstimo deve ser pago em 10 parcelas, digamos, com vencimento no dia 5 de cada mês, alguns meses tem 30 dias, outros 31, e o mês de fevereiro que pode ter 28 ou 29 dias. Ainda, as instituições financeiras geralmente não colocam a data de vencimento em sábados, domingos nem feriados e isso poderia aumentar ainda mais a variabilidade no intervalo de tempo entre as parcelas. Com tudo isso, cada diferença no intervalo provoca distorções no cálculo dos juros.
Outra limitação, no caso do Brasil, é que sobre várias modalidades de empréstimos incide um imposto chamado IOF. Muitas vezes, o cálculo do IOF também considera a quantidade de dias corridos, baseado em quanto tempo o dinheiro disponibilizado pela instituição financeira ficou na mão do cliente antes de ser devolvido na forma de pagamento de parcelas. E a fórmula da Tabela Price também teria alguns problemas, pois o próprio saldo devedor varia em função do tempo e agora também do IOF.
O exemplo a seguir usa o mesmo cenário do exemplo anterior, mas agora vai utilizar um cálculo diário de juros. Veremos como a variação da quantidade de dias entre o pagamento de uma parcela e a próxima afeta o saldo devedor ao final do pagametno da última parcela.
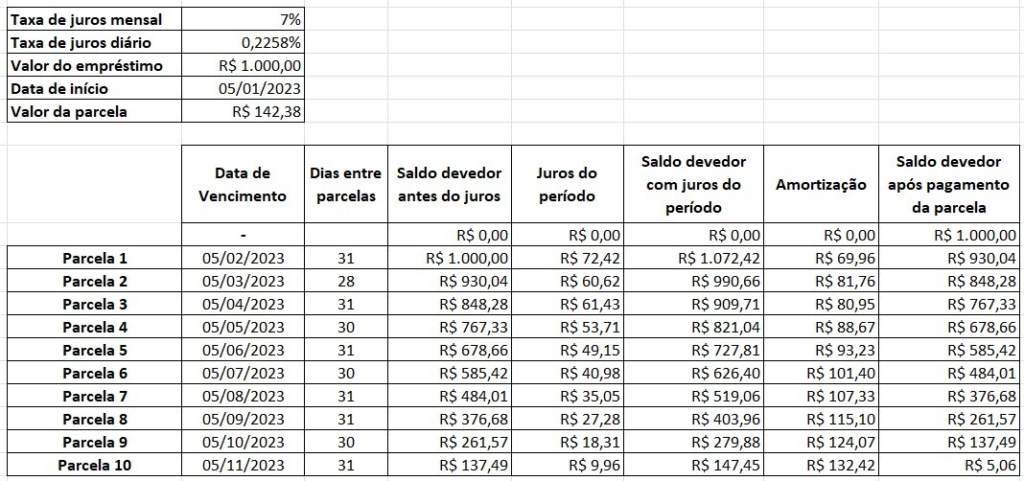
O saldo devedor não é zerado ao final da primeira parcela. Nesse caso, o pagamento das parcelas não foi suficiente, ficando um saldo de R$ 5,06 a ser pago. Também existem situações onde o valor das parcelas excede o que é necessário para zerar o financiamento. Dependendo também da quantidade de parcelas, da taxa de juros, essa distoção pode ser ainda maior. Isso tudo é provocado pela variabilidade no período de tempo o qual é aplicado o juros.
As instituições financeiras precisam usar o juros diário pois, quando um pagamento é antecipado ou atrasado, a diferença de juros que vai ser paga a mais ou menos é realizada levando em consideração a quantidade de dias. E por se tratar de juros compostos, os cálculos acabam ficando um pouco mais complexos que somar, subtrair, dividir e multiplicar.
O problema, então, é estabelecer um menicanismo que seja capaz de calcular o valor de parcela ideal usando a essência da Tabela Price, que é o pagamento de parcelas com valores iguais.
Um método numérico para aproximação do valor da parcela
Para contornar esses problemas, o cálculo numérico vem ao resgate. A ideia é usar o método da bisseção para alcançar uma aproximação para o valor da parcela que seja capaz de zerar o saldo devedor após o pagamento de todas as parcelas.
Este método busca encontrar um valor dentro de um intervalo possível. Como estamos tratando do valor da parcela, podemos garantir que ele será maior que zero, sendo o zero um bom valor para o início do nosso intervalo. Ainda, podemos dizer que valor da parcela vai ser menor que o valor do próprio empréstimo. Assim, para um empréstimo de R$ 1000,00, vamos estabelecer que o valor da parcela vai estar no intervalo compreendido entre R$ 0,00 e R$ 1000,00. Basta, agora, dentro desse intervalo escolher um valor para usarmos como primeira tentativa. No método da bisseção, vamos pegar o valor intermediário, isto é, R$ 500, para servir como primeira aproximação.
E tomando R$ 500,00 como o valor da parcela, o resultado é que, ao final do pagamento da última parcela, o saldo devedor estaria negativo. Negativo aqui significa que foi pago um valor além do que era devido e lembrando que o objetio é zerar o saldo devedor. A imagem a seguir mostra a memória do cálculo considerando o valor da parcela em R$ 500,00.

A partir disso é possível fazer uma análise. Se foi pago valor a mais, nenhum valor de parcela entre R$ 500,00 e R$ 1000,00 precisa ser considerado, uma vez que elevar o valor da parcela além dos R$ 500,00 apenas faria com que o saldo devedor ultrapasse ainda mais necessário. Logo, inicialmente tínhamos um intervalo compreendido entre R$ 0,00 e R$ 1000,00, e sabemos que R$ 500,00 foi um valor muito alto. Então basta que consideremos agora o intervalo entre R$ 0,00 e R$ 500,00. O processo se repete mais uma vez no método da bisseção para este novo e reduzido intervalo. O valor intermediário entre 0 e 500 é R$ 250,00. A memória do cálculo é apresentada a seguir.
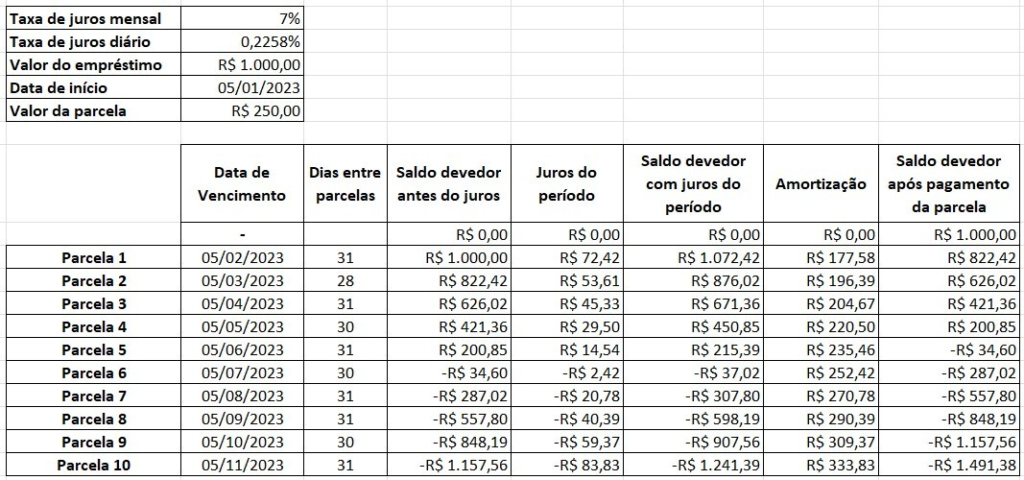
Melhorou um pouco. Na primeira tentativa, com valor de parcela de R$ 500,00, o saldo devedor ao final estava em negativos R$ 4967,74. Agora, com valor de parcela de R$ 250,00, o saldo devedor está em negativos R$ 1491,38. Assim, R$ 250,00 se mostrou um valor de parcela ainda muito alto. Portanto, qualquer valor de parcela acima de R$ 250,00 não precisa ser considerado e concluímos que o valor ideal está entre R$ 0,00 e R$ 250,00. E mais uma vez o processo da bisseção se repte. Agora, o valor intermediário entre R$ 0,00 e R$ 250,00 é R$ 125,00, que vai ser o novo valor de parcela. A memória do cálculo é apresentada a seguir.
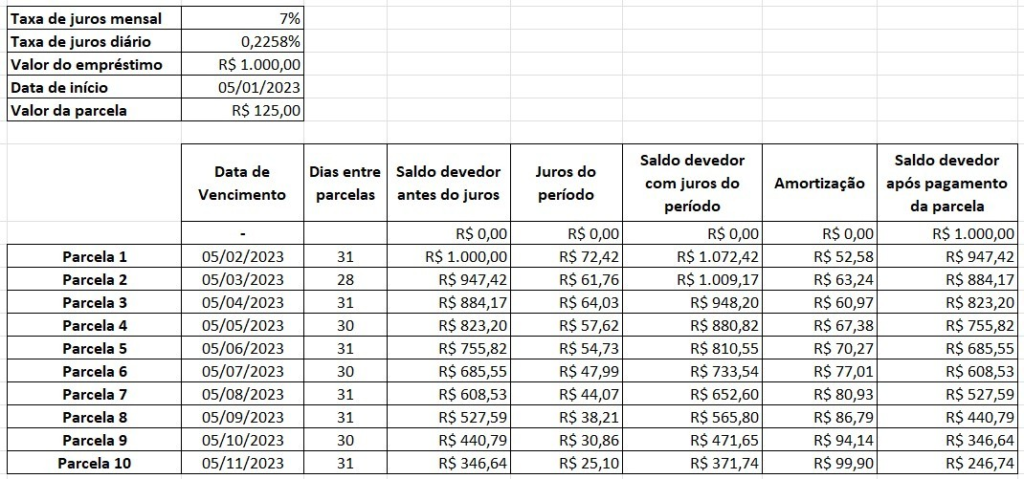
Com um valor de parcela de R$ 125,00, notamos que ao final do pagamento da ultima parcela, o empréstimo ainda possuia um saldo devedor positivo de 246,74 a ser pago. Isso indica que o valor de parcela em R$ 125,00 foi mais baixo que o necessário para zerar o saldo devedor do empréstimo. Desta forma, qualquer valor abaixo de R$ 125,00 também não serviria, pois baixar ainda mais o valor da parcela só aumentaria o saldo devedor, distanciando ele do zero. Assim, o valor ideal está no intervalor entre R$ 125,00 e R$ 250,00. Mais uma vez, o método da bisseção continua, pegando o valor intermediário desse novo e ainda mais reduzido intervalo, que é R$ 187,50. A memória do cálculo é apresentada a seguir.
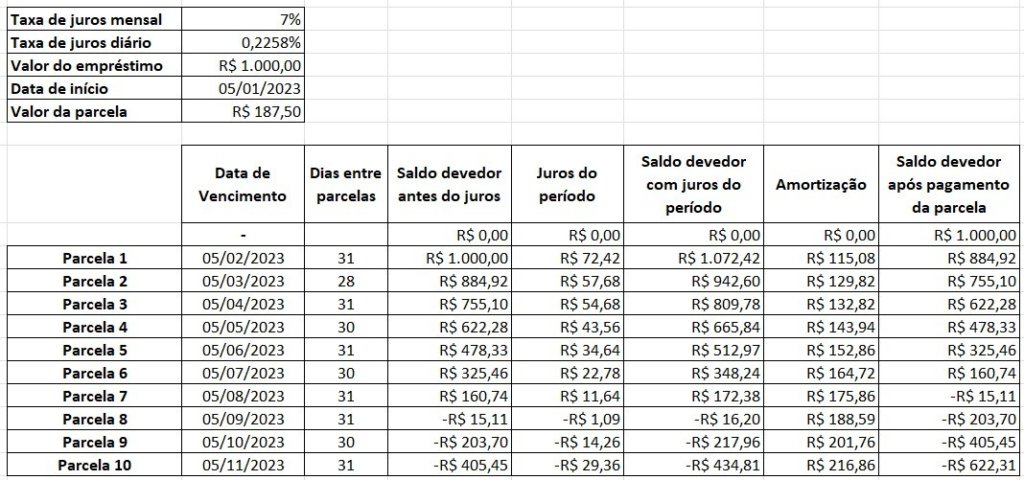
Mais uma vez o saldo devedor ficou negativo em R$ 622,21. A análise continuaria para reduzir ainda mais o intervalo. Após essa iteração, o novo intervalo seria entre R$ 125,00 e R$ 185,50. Lebrando que começamos com um intervalo que ia do zero até o 1000 e agora estamos em um intervalo de tamanho 60,5.
A fim de automatizar esse processo, um script de comptudor, em linguagem Kotlin, é apresetado a seguir e realiza a busca pelo valor de parcela usando o método da bisseção.
import java.time.LocalDat
import java.time.format.DateTimeFormatter
import java.time.temporal.ChronoUnit
fun String.toLocalDate() = LocalDate.from(
DateTimeFormatter.ofPattern("dd/MM/yyyy").parse(this)
)
fun main() {
val taxaJurosMensal = 0.07
val taxaJurosDiario = Math.pow(1 + taxaJurosMensal, 1.0 / 30) - 1
val valorEmprestimo = 1000.0
val datas = listOf(
"05/01/2023".toLocalDate(),
"05/02/2023".toLocalDate(),
"05/03/2023".toLocalDate(),
"05/04/2023".toLocalDate(),
"05/05/2023".toLocalDate(),
"05/06/2023".toLocalDate(),
"05/07/2023".toLocalDate(),
"05/08/2023".toLocalDate(),
"05/09/2023".toLocalDate(),
"05/10/2023".toLocalDate(),
"05/11/2023".toLocalDate(),
)
val valorParcela = calcularValorParcela(
montante = valorEmprestimo,
taxaJuros = taxaJurosDiario,
datas = datas
)
println("Valor parcela: $valorParcela")
}
fun calcularValorParcela(
montante: Double,
taxaJuros: Double,
// a primeira data da lista corrresponde a liberação do valor
// a segunda data é o vencimento da primeira parcela
datas: List<LocalDate>
): Double {
var inicioIntervalo: Double = 0.0
var finalIntervalo: Double = montante
var valorParcela: Double
while (true) {
var saldoDevedor = montante
valorParcela = (inicioIntervalo + finalIntervalo) / 2
repeat(datas.size - 1) { index ->
val diasEntreParcelas = ChronoUnit.DAYS.between(datas[index], datas[index + 1]).toDouble()
saldoDevedor = saldoDevedor * Math.pow(1 + taxaJuros, diasEntreParcelas)
saldoDevedor = saldoDevedor - valorParcela
}
if (finalIntervalo - inicioIntervalo <= 0.001) break
if (saldoDevedor > 0) inicioIntervalo = valorParcela
else finalIntervalo = valorParcela
}
return valorParcela
}Após a execução dessa rotina, chegamos a um vlaor de parcela de R$ 142,74, que é um pouco maior que o valor indicado inicialmente pela fórmula da Tabela Price. A imagem a seguir mostra que essa parcela é bem melhor, pois o saldo devedor ao final é bem próximo de zero.
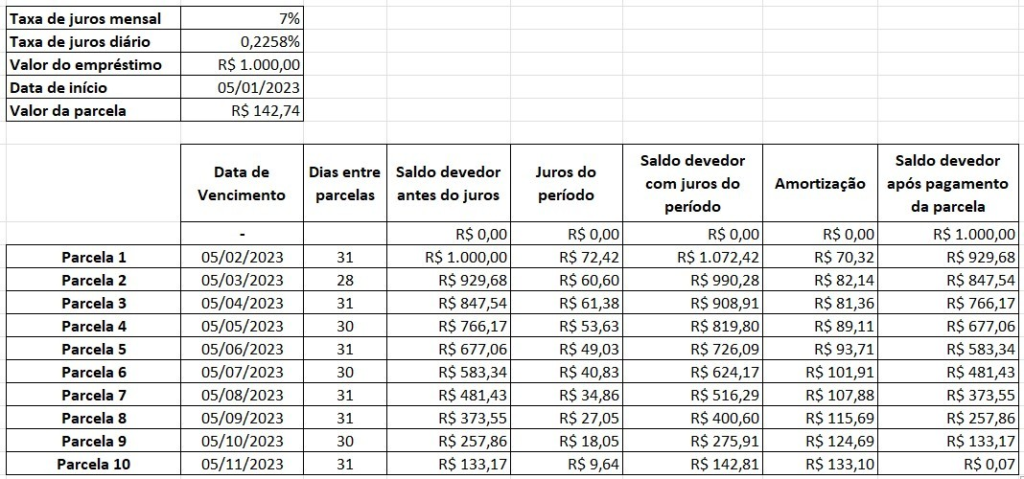
Foram necessárias 22 repetições, isto é, testar 22 valores de parcelas, sempre reduzindo o intervalo de possibilidades. O script foi programado para ser encerrado quando o intervalo onde estamos buscando o valor da parcela for menor que 0.001. Esse valor é uma boa aproximação, pois estamos lidando com valores monetários, que possuem 2 casas decimais. Ainda sobre o exemplo acima, onde o método trouxe um valor de parcela de R$ 142,74, o saldo devedor ficou positivo em 7 centavos. Isso é um problema do arredondamento para 2 casas decimais. A rotina é capaz de encontrar um valor de parcelas R$ 142,74546, que zeraria o saldo devedor. No entanto, não é possível, uma vez que valores monetários, pelo menos dentro do contexto desse artigo, usam 2 casas decimais, apenas.
O exemplo seguinte foi montado para criar diferenças muito grandes e bastante variadas nos períodos entre as parcelas. Mesmo assim é possível aplicar o método de amortização Price com o auxílio do script. Ele encontra o valor de parcela de R$ 159,78.

Conclusão
Como método computacional, usar a bisseção para aproximar o melhor valor de parcela é fácil de implementar.
Por outro lado, por se tratar de um método essencialmente iterativo, em alguns casos pode ser um desafio escalar esse processo em alta demanda, uma vez que é necessário realizar diversas repetições de rotinas computacionais.
Ainda, o método da forma como foi implementado, não aborda os casos do cálculo do imposto IOF, que incide sobre operações de empréstimo. Uma rotina computacional para atender esse tipo de necessidade pode ser abordada em melhorias dessa técnica.
Mas como solução básica para cálculo de parcela em Tabela Price, usar o método da bisseção garante que sempre chegaremos em um resultado em um tempo computacional razoavelmente determinado, pois o intervalo de possibilidades sempre será divido por 2 e rapidamente se torna tão pequeno quanto necessário. E, também, ao usar o método da bisseção, essa técnica permite total flexibilidade no prazo de pagamento, aceitando qualquer intervalo de tempo entre as parcelas.
Referências
Neste artigo, eu contei com informações dos seguintes locais
https://pt.wikipedia.org/wiki/Tabela_Price
https://brasilescola.uol.com.br/matematica/calculo-numerico.htm
https://www1.univap.br/spilling/CN/CN_IntroEmenta.pdf
https://www.ufrgs.br/reamat/CalculoNumerico/livro-py/sdeduv-metodo_da_bissecao.html