A eficiência de uma engine de xadrez tem uma relação muito íntima com a qualidade de seu mecanismo de geração de movimentos. Essas rotinas são responsáveis por enumerar todos os movimentos possíveis a partir de uma posição específica no tabuleiro, servindo como base para a avaliação e seleção das melhores jogadas. Essensiclamente, uma engine faz uma busca em várias possibilidades, calculando alguns lances à frente. Por ser um computador, claro, tudo isso é feito extremamente rápido.
Quando se fala em eficiência do mecanismo de geração de movimentos, fala-se em quão rápido os movimentos disponíveis são encontrados. Até onde uma dama pode mover sem ir além de um destino bloqueado por um peão da mesma cor? A casa para onde o rei pretende mover está sob ataque de uma peça advesária? Como sabemos, um jogador não pode colocar o próprio rei em xeque. Quanto mais rápido isso é feito, mais tempo sobra para o computador usar em realizar esses movimentos e calcular mais jogadas a partir das novas posições.
E para uma engine de xadrez existe uma técnica fundalmente: bitboards. É uma forma de representar usando bits, a menor unidade de informação em um computador moderno comum (não quântico). E com isso, uma grata coincidência! Os processadores da grande maioria dos dispositivos eletrônicos comumente usados pelas pessoas utilizam arquitetura de 64 bits. Mesmo telefones celulares de entrada, ou computadores menos parrudos, usam processadores de 64 bits. Um tabuleiro de xadrez tem 64 casas e, como veremos, isso facilita muito as coisas.
Como representar um tabuleiro de xadrez dentro do computador? Já mencionei que é com bitboards. Mas se tivesse que programar algo assim sem qualquer requisito de velocidade, como faria? Qual primeira ideia vem à mente? Um tabuleiro de xadrez é uma matriz com 8 linhas e 8 colunas. Uma array de 2 dimensões é uma solução natural e está disponível em muitas linguagens de programação. Em linguagem C, podemos fazer algo como mostrado abaixo.
char board[8][8];
// considerando que a dama é representada pelo caractere 'q' dama preta e 'Q' para a dama branca
// a dama preta na casa C4 pode ser algo tão simples quanto
board[4][2] = 'q';
// e a dama branca na case F6
board[2][6] = 'Q';Com base nessa estrutura usando um array, basta deixar a imaginação trabalhar. Mover a dama de casa é simplesmente colocar o caractere que a representa em outra posição do array, sem esquecer de colocar algo que representa casa vazia na posição de origem. Cada peça tem sua forma própria de movimentar e os algoritmos devem considerar todas as regras já bem conhecidas do xadrez.
Bitboards
Bitboards são uma outra forma de representar o tabuleiro. É bem mais eficiente que um simples array. Um bitboard nada mais é que um número de 64 bits. Em linguagem Java, um tipo long tem 64 bits, em C, long long int (ou unsigned long long int), e em Kotlin Long (ou ULong).

Cada tipo de peça tem o seu próprio bitboard e usamos dois bitboards extras para indicar as cores. No tabuleiro abaixo, o bitboard dos cavalos deve estar com o quarto bit com valor 1 para indicar que há um cavalo naquela casa. Igualmente, o bitboard das peças pretas deve ter o valor 1 no quarto bit para indicar que a peça é preta.

A maioria das linguagens permite manipulação de bits específicos. Se a existência de uma peça em uma posição é indicada por um bit, manipular esse bit específico é especialmente útil para remover ou colocar a peça nessa posição.
// em linguagem Kotlin, podemos fazer algo parecido com o seguinte:
typealias Bitboard = ULong
var blacks: Bitboard
var whites: Bitboard
var pawns: Bitboard
var knights: Bitboard
var bishops: Bitboard
var rooks: Bitboard
var queens: Bitboard
var kings: BitboardAssim, precisamos construir operações capazes de listar os movimentos disponíveis para uma data posição. Os bitboards devem ser acrescentados com outras estruturas auxiliares para permitir movimentos com roque, en passant e promoção do peão. Veremos cada uma dessas operações em artigos futuros.
Movimentos pseudo-válidos
O xadrez tem regras muito claras sobre o movimento das peças. Uma, em especial, não permite que um movimento coloque o próprio rei perigo. Isso faz bastante sentido quando pensamos que se o rei for capturado, o jogador desse rei perde o jogo. No entanto, uma técnica muito utilizada pelas engines é gerar os chamados movimentos pseudo válidos. São movimentos cuja regra de colocar o rei em perigo não foi verificada. O movimento é listado como qualquer outro.
Existe um bom motivo para isso! Quando a engine está calculando qual próximo movimento deve ser feito em uma partida, ela calcula muita coisa. Vamos supor que a partir de uma posição qualquer existam 15 movimentos disponíveis para o jogador da vez. É possível que a engine não teste todos esses movimentos. Ela pode escolher realizar apenas alguns usando critérios previamente programados. Assim, a engine valida o movimento apenas se ele realmente for escolhido para ser jogado. Se ele não for um movimento válido, a engine não realiza ele e passa para o teste do próximo. Com isso, ao gerar os 15 movimentos inicialmente listados, a engine economiza tempo ao não validar eles e, caso não considere todos esses movimentos no cálculo, aqueles não validados produzem uma economia de tempo considerável.
Para o movimento do cavalo, rei, cavalo e peão, serão gerados apenas movimentos pseudo-válidos. As técnicas para validar um movimento serão abordadas em artigos futuros.
Movimento do cavalo
A ideia é gerar uma base de destinos pré calculados para o cavalo. A partir de uma casa, o cavalo tem destinos fixos. Não é como uma peça dama, que pode mover uma quantidade arbitrária de casas à critério do jogador. Devemos apenas tomar o cuidado para que o valor não ocupe uma casa ocupada por uma peça da mesma cor.
O tabuleiro abaixo ilustra como deve ser a base de destinos pré calculados. Cada circulo indica um possível destino para o cavalo posicionado espeficicamente na casa e5. Isso também é um bitboard! Cada possível destino é indicado com o bit 1, enquanto todos os outros devem ter bitos com valor 0. Devemos ter 64 bitboards desse tipo, cada um para uma possível cada de origem do cavalor.
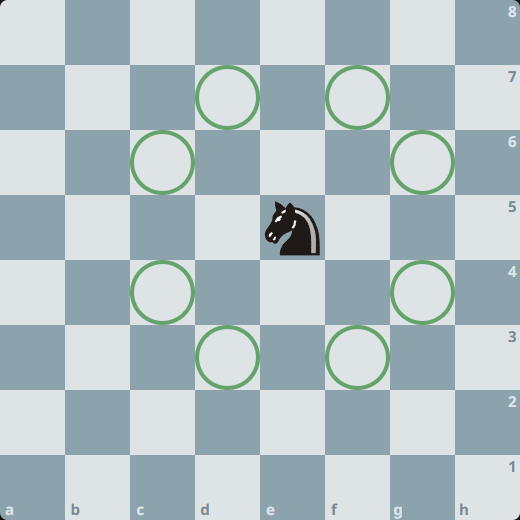
Por que é útil ter esses destinos pré calculados? Vamos lembrar que o tabuleiro é representado por bitboards para cada peça e 2 bitboards para cada cor. Podemos listar os destinos do cavalo apenas fazendo simples operações bit a bit. Usamos uma operação de negação bit a bit (~) para remover as casas que são ocupadas por peças da mesma cor do cavalo. Daí bastar fazer um end entre os possíveis destinos e toda as outras casas. Essas operações bit a bit usam menos ciclos de CPU. Uma alternativa com array possivelmente usaria algoritmos com iteração, verificação de condições de controle, etc. Cada iteração usaria tempo precioso da CPU, que pode ser economizado ao aplicar algoritmos que fazem uso dos bitboards.
// cosiderando que é um cavalo preto que está movendo
Bitboard ownPieces = blacks
Bitboard knightTargets = knightMoveDatabase[e5] & ~ownPieces
// os bits ativos da variável knightTargets indicam as possíveis casas de destino do cavalo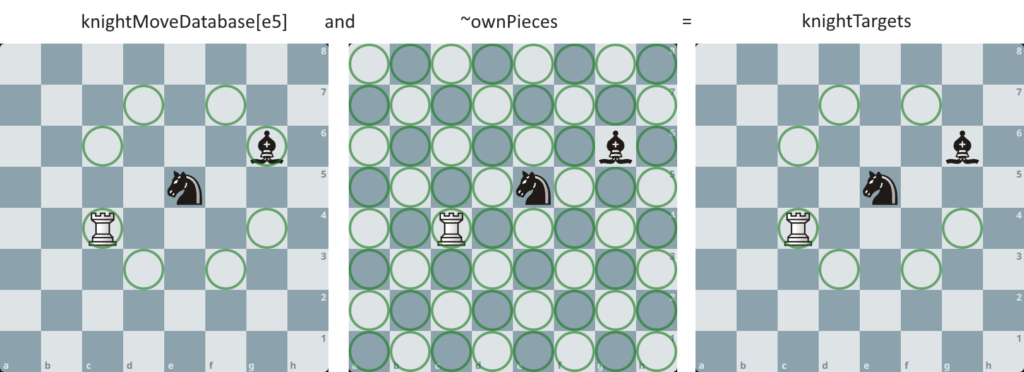
Para o cavalo, a base de destinos pré calculos seria algo como o código apresentado abaixo.
knightMoveDatabase = int64_array[64]
knightMoveDatabase[0] = 0x0020400000000000
knightMoveDatabase[1] = 0x0010A00000000000
knightMoveDatabase[2] = 0x0088500000000000
knightMoveDatabase[3] = 0x0044280000000000
knightMoveDatabase[4] = 0x0022140000000000
knightMoveDatabase[5] = 0x00110A0000000000
knightMoveDatabase[6] = 0x0008050000000000
knightMoveDatabase[7] = 0x0004020000000000
knightMoveDatabase[8] = 0x2000204000000000
knightMoveDatabase[9] = 0x100010A000000000
knightMoveDatabase[10] = 0x8800885000000000
knightMoveDatabase[11] = 0x4400442800000000
knightMoveDatabase[12] = 0x2200221400000000
knightMoveDatabase[13] = 0x1100110A00000000
knightMoveDatabase[14] = 0x0800080500000000
knightMoveDatabase[15] = 0x0400040200000000
knightMoveDatabase[16] = 0x4020002040000000
knightMoveDatabase[17] = 0xA0100010A0000000
knightMoveDatabase[18] = 0x5088008850000000
knightMoveDatabase[19] = 0x2844004428000000
knightMoveDatabase[20] = 0x1422002214000000
knightMoveDatabase[21] = 0x0A1100110A000000
knightMoveDatabase[22] = 0x0508000805000000
knightMoveDatabase[23] = 0x0204000402000000
knightMoveDatabase[24] = 0x0040200020400000
knightMoveDatabase[25] = 0x00A0100010A00000
knightMoveDatabase[26] = 0x0050880088500000
knightMoveDatabase[27] = 0x0028440044280000
knightMoveDatabase[28] = 0x0014220022140000
knightMoveDatabase[29] = 0x000A1100110A0000
knightMoveDatabase[30] = 0x0005080008050000
knightMoveDatabase[31] = 0x0002040004020000
knightMoveDatabase[32] = 0x0000402000204000
knightMoveDatabase[33] = 0x0000A0100010A000
knightMoveDatabase[34] = 0x0000508800885000
knightMoveDatabase[35] = 0x0000284400442800
knightMoveDatabase[36] = 0x0000142200221400
knightMoveDatabase[37] = 0x00000A1100110A00
knightMoveDatabase[38] = 0x0000050800080500
knightMoveDatabase[39] = 0x0000020400040200
knightMoveDatabase[40] = 0x0000004020002040
knightMoveDatabase[41] = 0x000000A0100010A0
knightMoveDatabase[42] = 0x0000005088008850
knightMoveDatabase[43] = 0x0000002844004428
knightMoveDatabase[44] = 0x0000001422002214
knightMoveDatabase[45] = 0x0000000A1100110A
knightMoveDatabase[46] = 0x0000000508000805
knightMoveDatabase[47] = 0x0000000204000402
knightMoveDatabase[48] = 0x0000000040200020
knightMoveDatabase[49] = 0x00000000A0100010
knightMoveDatabase[50] = 0x0000000050880088
knightMoveDatabase[51] = 0x0000000028440044
knightMoveDatabase[52] = 0x0000000014220022
knightMoveDatabase[53] = 0x000000000A110011
knightMoveDatabase[54] = 0x0000000005080008
knightMoveDatabase[55] = 0x0000000002040004
knightMoveDatabase[56] = 0x0000000000402000
knightMoveDatabase[57] = 0x0000000000A01000
knightMoveDatabase[58] = 0x0000000000508800
knightMoveDatabase[59] = 0x0000000000284400
knightMoveDatabase[60] = 0x0000000000142200
knightMoveDatabase[61] = 0x00000000000A1100
knightMoveDatabase[62] = 0x0000000000050800
knightMoveDatabase[63] = 0x0000000000020400Movimento do rei
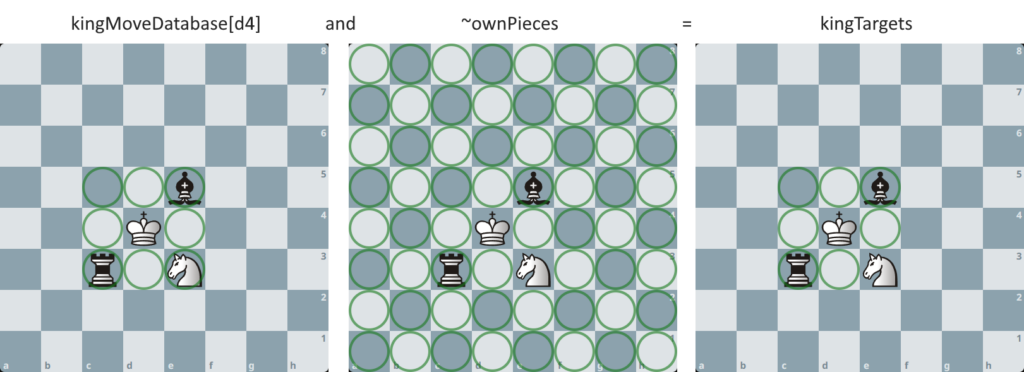
Para gerar os possíveis destino do rei, a ideia é exatamente a mesma do cavalo. As operações bit a bit são as mesmas. A única coisa que muda é a base de destinos pré calculados, que agora serão 64 bitboardas montados de acordo com o padrão de movimento do rei. Vale lembrar que são movimentos pseudo válidos e o movimento de roque não é abordado aqui.
Movimento do peão
Para o peão, as coisas mudam um pouco. Enquanto o rei e o valor conseguem mover livremente no tabuleiro, em todas as direções, o peão se move apenas para frente, dependendo do ponto de vista das peças pretas ou brancas. Além disso, o peão se move para frente, captura em diagonal, captura en passant, e pode mover duas casas quando está na posição inifial. E, finalmente, durante a promoção, um movimento do peão na verdade geram 4 lances possíveis, que são as peças para as quais o peão pode prover (dama, torre, bispo, cavalo).
Um pouco de mudança na estratégia, mas com a ideia essencialmente igual. Continuamos usando uma base de destinos pré calculados, mas agora serão várias bases diferentes, uma para cada situação. Para o en passant, usamos um bitboard com o bit ativo indicando o destino onde o peão vai se mover. Este bitboard atua uma emulação do peão inimigo presente naquela casa, mas que efetivamente, não está lá. Ressaltamos que este bitboard é atualizado sempre que uma captura em passant está disponível, ou não.
// exemplo de código em linguagem Kotlin para encontrar os targets do peão
val (
singleMoveMask,
doubleMoveMask,
captureMoveMask,
oppositePiecesOccupancy,
flagsMask
) = when (movingPieceColor) {
BLACK -> ulongArrayOf(
blackPawnSingleMoveMask[originSquare.index],
blackPawnDoubleMoveMask[originSquare.index],
blackPawnCaptureMoveMask[originSquare.index],
whites,
ROW_5_SET,
)
WHITE -> ulongArrayOf(
whitePawnSingleMoveMask[originSquare.index],
whitePawnDoubleMoveMask[originSquare.index],
whitePawnCaptureMoveMask[originSquare.index],
blacks,
ROW_2_SET,
)
}
val occupancy = getOccupancy()
val singleMove = singleMoveMask
.and(occupancy.inv())
val doubleMove = doubleMoveMask
.and(occupancy.inv())
.and(singleMove.shift(8 * -movingPieceColor.direction))
val captureMove = captureMoveMask
.and(oppositePiecesOccupancy.or(flagsMask.and(flags)))
return singleMove or doubleMove or captureMoveConclusão
A utilização de bitboards na programação de engines de xadrez representa um salto significativo em termos de eficiência e desempenho. Essa abordagem não apenas simplifica a representação do tabuleiro, mas também permite operações de geração de movimentos incrivelmente rápidas, utilizando manipulação direta de bits. Ao substituir estruturas tradicionais de arrays por bitboards, reduzimos o tempo de execução das rotinas críticas, liberando mais recursos computacionais para análises mais profundas e precisas durante a partida.
A pré-calculação de destinos de peças como cavalo, rei e peão é um exemplo claro de como o uso inteligente de operações bit a bit pode otimizar a busca por movimentos, economizando ciclos de CPU que seriam desperdiçados em verificações repetitivas. Esse nível de otimização é vital para que uma engine possa competir em alto nível, realizando cálculos em profundidade sem comprometer a velocidade de resposta.

