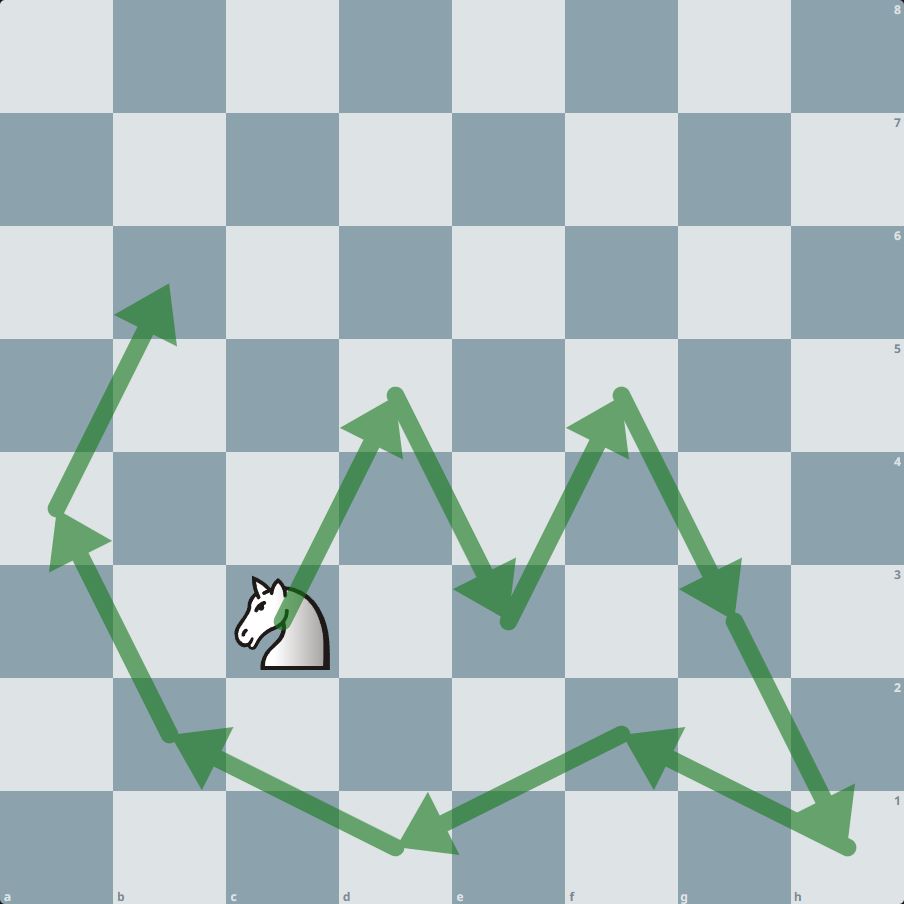
Quem joga xadrez conhece a forma do movimento do cavalo. Ele faz uma espécis de L.
Neste problema, todas as casas do tabuleiro devem ser visitadas pelo cavalo, sem repetir casas. O cavalo pode terminar o percurso em uma casa onde seja possivel alcançar a casa inicial no próximo movimento. Este cenário é chamado de caminho fechado, pois forma uma espécie de círculo. A outra forma é o caminho aberto, onde os casas de início e fim não conseguem se conectar diretamente.
Backtracking
Backtracking é uma técnica aplicável na solução de problemas de satisfação de restrições. Basicamente, a ideia é construir a solução de maneira gradual, observando todas as restrições a cada etapa. A solução de alguns problemas com backtracking geralmente usa uma lógica com recursividade. É importante notar que backtracking usa recursividade como uma maneira para implementar a solução. A recursividade por sí só não representa backtracking.
Em determinadas situações, testar todas as possibilidades é uma solução factível, muito mais útil que montar uma lógica complexa que resolva o problema. Uma solução inicial é expandida e novos elementos são adicionados. A cada iteração o algoritmo verifica se todas as restrições são atendidas. Assim, backtracking é uma técnica generalista que precisa ser adaptada para as necessidades de cada problema. No final, encontra-se uma solução, ou não, após testar tudo.
Para o problema do caminho do cavalo, fica evidente o quão naturalmente a solução pode ser encontrada ao se usar backtracking. Quando tentatamos resolver o problema por nós mesmos, uma forma de buscar uma solução é testar alguns caminhos, progredindo até quando percebemos que o cavalo está preso. Nesse ponto, dificilmente iniciamos a solução do zero. Preferimos voltar algumas casas e continuar dali.
Solução
O algoritmo inicia posicionando a peça em uma casa do tabuleiro, marca essa casa como ocupada e busca testar o próximo movimento a partir dessa casa. Daí basta repetir o processo. Sempre que uma restrição não for atendida, o algoritmo desfaz o caminho feito e tenta outro movimento. A natureza recursiva da solução fica responsável por desfazer caminhos que já foram testados.
A implementação abaixo busca a solução movimentando o cavalo de maneira aleatória entre as opções disponíveis até que todas as opções acabem. Adicionei o fator aleatório porque percebi que algumas soluções eram encontradas em alguns milissegundos por pura coincidência, isto é, a maneira como programei, ao testar alguns caminhos primeiro, encontrava uma solução rapidamente.
import kotlin.random.Random
import kotlin.time.measureTimedValue
class KnightPath(
val boardSideSize: Int,
val startRow: Int,
val startColumn: Int
) {
private val rdn = Random(System.nanoTime())
private val boardSize = boardSideSize * boardSideSize
private val path = Array(boardSideSize) {
Array(boardSideSize) { EMPTY }
}
fun findPath(): List<Pair<Int, Int>> {
path.forEach { a -> a.forEachIndexed { index, _ -> a[index] = EMPTY } }
path[startRow][startColumn] = 0
if (findPath(startRow, startColumn, 1)) {
return path.flatMapIndexed { indexX, row ->
row.mapIndexed { indexY, y -> y to Pair(indexX, indexY) }
}.sortedBy { it.first }
.map { it.second }
}
return emptyList()
}
private fun findPath(x: Int, y: Int, step: Int): Boolean {
if (step == boardSize) {
return true
}
val r = rdn.nextInt(1000000)
for (shiftIndex in 0..7) {
val idx = (r + shiftIndex) % 8
val tX = x + shifts[0][idx]
val tY = y + shifts[1][idx]
if (
tX !in 0 until boardSideSize
|| tY !in 0 until boardSideSize
|| path[tX][tY] != EMPTY
) {
continue
}
path[tX][tY] = step
if (findPath(tX, tY, step + 1)) {
return true
}
path[tX][tY] = EMPTY
}
return false
}
companion object {
private const val EMPTY = -1
private val shifts = arrayOf(
intArrayOf(-2, -2, -1, -1, +1, +1, +2, +2),
intArrayOf(-1, +1, -2, +2, -2, +2, -1, +1),
)
}
}
fun main() {
val tests = 1
measureTimedValue {
val rdn = Random(System.nanoTime())
val boardSideSize = 7
repeat(tests) {
val startRow = 0
val startColumn = 0
KnightPath(
boardSideSize = boardSideSize,
startRow = 0,
startColumn = 0
).findPath()
.apply {
if (isEmpty()) println("No solution found starting in [$startRow, $startColumn]")
}
.forEachIndexed { index, pair ->
println("#${index + 1} - [${pair.first}, ${pair.second}]")
}
}
}.duration.inWholeMilliseconds.run {
println("Duration: ${this / tests} ms")
}
}
Ao testar essa solução, no entanto, notei que ela não era performática. Mesmo buscando os caminhos de maneira aleatória, iniciando o caminho em determinadas casas fazia com que a solução demorasse muito a ser encontrada. Em tabuleiros de tamanho 8×8, o algoritmo continua a procurar mesmo depois de várias horas.
Tive que implementar uma técnica chamada de Heurística de Warnsdorff. A partir de uma posição, o algoritmo vai testar primeiro o movimento que leva à menor quantidade de opções no movimento subsequente. Isso reduz bastante quantidade de caminhos que precisam ser testando, provocando que uma solução seja encontrada mais rapidamente. Em outras palavras, se o cavalo está na posição X e tem como opção as casas A, B e C para mover, ele vai testar primeiro a casa A se, a partir dela, o cavalo conseguir ir a menos locais do que se estivesse em C ou B.
import kotlin.random.Random
import kotlin.time.measureTimedValue
class KnightPath(
val boardSideSize: Int,
val startRow: Int,
val startColumn: Int
) {
private val boardSize = boardSideSize * boardSideSize
private val availableMoves = Array(8) {
Array(3) { 0 }
}
private val path = Array(boardSideSize) {
Array(boardSideSize) { EMPTY }
}
fun findPath(): List<Pair<Int, Int>> {
path.forEach { a -> a.forEachIndexed { index, _ -> a[index] = EMPTY } }
path[startRow][startColumn] = 0
if (findPath(startRow, startColumn, 1)) {
return path.flatMapIndexed { indexX, row ->
row.mapIndexed { indexY, y -> y to Pair(indexX, indexY) }
}.sortedBy { it.first }
.map { it.second }
}
return emptyList()
}
private fun findPath(x: Int, y: Int, step: Int): Boolean {
if (step == boardSize) {
return true
}
val totalMoves = generateMovesByWarnsdorffHeuristic(x, y)
for (moveIndex in 0 until totalMoves) {
val move = availableMoves[moveIndex]
path[move[0]][move[1]] = step
if (findPath(move[0], move[1], step + 1)) {
return true
}
path[move[0]][move[1]] = EMPTY
}
return false
}
private fun generateMovesByWarnsdorffHeuristic(x: Int, y: Int): Int {
var foundMoves = 0
for (shiftIndex in 0..7) {
val tx = x + shifts[0][shiftIndex]
val ty = y + shifts[1][shiftIndex]
if (!isSafe(tx, ty)) {
continue
}
var counter = 0
for (shiftIndex2 in 0..7) {
if (
isSafe(
tx + shifts[0][shiftIndex2],
ty + shifts[1][shiftIndex2]
)
) {
counter++
}
}
availableMoves[foundMoves][0] = tx
availableMoves[foundMoves][1] = ty
availableMoves[foundMoves][2] = counter
foundMoves++
}
(foundMoves until availableMoves.size).forEach { i ->
availableMoves[i][2] = Int.MAX_VALUE
}
availableMoves.sortBy { it[2] }
return foundMoves
}
private fun isSafe(x: Int, y: Int): Boolean {
return (x in 0 until boardSideSize)
&& y in (0 until boardSideSize)
&& path[x][y] == EMPTY
}
companion object {
private const val EMPTY = -1
private val shifts = arrayOf(
intArrayOf(-2, -2, -1, -1, +1, +1, +2, +2),
intArrayOf(-1, +1, -2, +2, -2, +2, -1, +1),
)
}
}
fun main() {
val tests = 5
measureTimedValue {
val boardSideSize = 8
repeat(tests) {
val startRow = Random.nextInt(boardSideSize)
val startColumn = Random.nextInt(boardSideSize)
KnightPath(
boardSideSize = boardSideSize,
startRow = startRow,
startColumn = startColumn
).findPath()
.apply {
if (isEmpty()) println("No solution found starting in [$startRow, $startColumn]")
}
.forEachIndexed { index, pair ->
println("#${index + 1} - [${pair.first}, ${pair.second}]")
}
}
}.duration.inWholeMilliseconds.run {
println("Duration: ${this / tests} ms")
}
}
A busca por uma solução no tabuleiro 8×8 que levaria várias horas numa implementação mais simples, terminou em alguns milissegundos usando a Heurística de Warnsdorff. Conseguiu encontrar soluções para tabuleiros bem maiores, como 1000×1000 (1 milhão de casas), que custou apenas 6 segundos.
Conclusão
Força bruta é uma solução para diversos problemas computacionais e backtracking é uma das formas de implementar essa solução. Por testar todas as possibilidades, a busca eventualmente alcança uma solução ótima.
No entanto, a complexidade de tempo necessária à execução do programa pode se tornar um fator crítico. O tempo necessário pode não ser factível mesmo para pequenas instâncias. Conhecer o domínio do problema que está sendo resolvido é importante, uma vez que dependendo da quantidade de estados possíveis, o algoritmo pode ser muito caro do ponto de vista de tempo. Assim, conhecer o problema possibilita a aplicação de otimizações, como a Heurística de Warnsdorff no caminho do cavalo, fazendo que caminhos que não levam a uma solução nem sejam avaliados, ou escolhendo caminhos melhores primeiro.
Outro fator importante do trabalho com backtracking é assumir o seu caráter ad doc, ou seja, cada solução precisa ser implementada individualmente. Backtracking é uma técnica de tentativa e erro na construção da solução. As restrições que devem ser atendidas, como o modelo computacional vai ser construído, como a construção das soluções parciais vai ser realizada é uma especificidade de cada problema.
Com tudo isso, backtracking apresenta-se como uma solução válida para o problema do caminho do cavalo. Consequentemente, vários outros problemas que podem ter uma solução geral construída a partir de soluções parciais, ou ainda, cuja as configurações possíveis possam ser todas testadas, podem ser resolvidos com backtracking se bem implementadas, sempre levando-se em consideração o fator do tempo.
Referências
- Artificial Intelligence – A Modern Approach, 4 ed., de Stuart Russell e Peter Norvig, publicado pela Pearson. Para adquirir o livro na Amazon Brasil: link
- Programming Challenges: The Programming Contest Training Manual, 1 ed, de Steven S. Skiena e Miguel A. Revila, publicado pela Springer. Para adquirir o livro na Amazon Brasil: link
- HEURÍSTICA EFICIENTE PARA O PASSEIO ABERTO DO CAVALO A PARTIR DE CASAS ARBITRÁRIAS EM TABULEIROS QUADRADOS, por Vitor Silva Costa e Vinícius Gusmão Pereira de Sá. Artigo disponível no em link